Week 7 Assignment Hypothesis Test for the Mean-Populations Standard Deviation Known
Question
Jamie, a bowler, claims that her bowling score is less than 168 points, on average. Several of her teammates do not believe her, so she decides to do a hypothesis test, at a 1% significance level, to persuade them. She bowls 17 games. The mean score of the sample games is 155 points. Jamie knows from experience that the standard deviation for her bowling score is 19 points.
- H0: μ≥168; Ha: μ<168
- α=0.01(significance level)
What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?
Question
Lexie, a bowler, claims that her bowling score is more than 140 points, on average. Several of her teammates do not believe her, so she decides to do a hypothesis test, at a 5% significance level, to persuade them. She bowls 18 games. The mean score of the sample games is 155 points. Lexie knows from experience that the standard deviation for her bowling score is 17 points.
- H0: μ≤140; Ha: μ>140
- α=0.05(significance level)
What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?
Question
Jamie, a chef, claims that her meatball weight is more than 3 ounces, on average. Several of her customers do not believe her, so she decides to do a hypothesis test, at a 5% significance level, to persuade them. She cooks 13 meatballs. The mean weight of the sample meatballs is 3.6 ounces. Jamie knows from experience that the standard deviation for her meatball weight is 0.5 ounces.
- H0: μ≤3; Ha: μ>3
- α=0.05(significance level)
What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?
Provide your answer below:
Question
Suppose a bowler claims that her bowling score is less than 116 points, on average. Several of her teammates do not believe her, so the bowler decides to do a hypothesis test, at a 5% significance level, to persuade them. She bowls 25 games. The mean score of the sample games is 103 points. The bowler knows from experience that the standard deviation for her bowling score is 19 points.
- H0: μ≥116; Ha: μ<116
- α=0.05(significance level)
What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?
Question
Which of the following results in a null hypothesis p≤0.61 and alternative hypothesis p>0.61?
Select the correct answer below:
Question
Which graph below corresponds to the following hypothesis test?
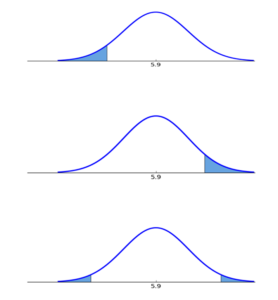
H0:μ≥5.9, Ha:μ<5.9
Question
Which of the following results in a null hypothesis p≥0.44 and alternative hypothesis p<0.44?
Question
Determine the Type II error if the null hypothesis, H0, is: a wooden ladder can withstand weights of 250 pounds and less.
Select the correct answer below:
You think the ladder can withstand weight of 250 pounds and less when, in fact, it cannot.
You think the ladder cannot withstand weight of 250 pounds and less when, in fact, it really can.
You think the ladder can withstand weight of 250 pounds and less when, in fact, it can.
You think the ladder cannot withstand weight of 250 pounds and less when, in fact, it cannot.
Question
Which graph below corresponds to the following hypothesis test?
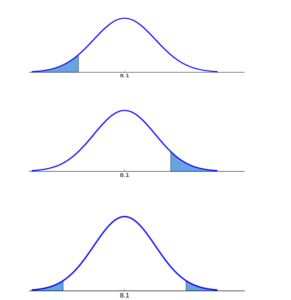
H0:p≤8.1, Ha:p>8.1
Question
Determine the Type I error if the null hypothesis, H0, is: an electrician claims that no more than 10% of homes in the city are not up to the current electric codes.
Select the correct answer below:
The electrician thinks that no more than 10% of homes in the city are not up to the current electrical codes when, in fact, there really are no more than 10% that are not up to the current electric codes.
The electrician thinks that more than 10% of the homes in the city are not up to the current electrical codes when, in fact, there really are more than 10% of the homes that do not meet the current electric codes.
The electrician thinks that more than 10% of the homes in the city are not up to the current electrical codes when, in fact, at most 10% of the homes in the city are not up to the current electric codes.
The electrician thinks that no more than 10% of homes in the city are not up to the current electrical codes when, in fact, more than 10% of the homes are not up to the current electric codes.
Question
Which of the following results in a null hypothesis p≤0.69 and alternative hypothesis p>0.69?
A mechanic wants to show that the percentage of car owners that follow a normal maintenance schedule is not 69%, contrary to a study that found that the percentage was 69%.
A mechanic wants to show that more than 69% of car owners follow a normal maintenance schedule, contrary to a study that found that the percentage was at most 69%.
A mechanic wants to show that at most 69% of car owners follow a normal maintenance schedule, contrary to a study that found that the percentage was more than 69%.
A mechanic wants to show that less than 69% of car owners follow a normal maintenance schedule, contrary to a study that found that the percentage was at least 69%.
Question
Which of the following results in a null hypothesis p≤0.47 and alternative hypothesis p>0.47?
Question
Which of the following results in a null hypothesis μ≤7 and alternative hypothesis μ>7?
Select the correct answer below:
A study wants to show that the mean number of hours of sleep the average person gets each day is at least 7.
A study wants to show that the mean number of hours of sleep the average person gets each day is 7.
A study wants to show that the mean number of hours of sleep the average person gets each day is more than 7.
A study wants to show that the mean number of hours of sleep the average person gets each day is at most 7.
Question
Suppose the null hypothesis, H0, is: a sporting goods store claims that at least 70% of its customers do not shop at any other sporting goods stores. What is the Type I error in this scenario?
Select the correct answer below:
The sporting goods store thinks that less than 70% of its customers do not shop at any other sporting goods stores when, in fact, less than 70% of its customers do not shop at any other sporting goods stores.
The sporting goods store thinks that at least 70% of its customers do not shop at any other sporting goods stores when, in fact, at least 70% of its customers do not shop at any other sporting goods stores.
The sporting goods store thinks that less than 70% of its customers do not shop at any other sporting goods stores when, in fact, at least 70% of its customers do not shop at any other sporting goods stores.
The sporting goods store thinks that at least 70% of its customers do not shop at any other sporting goods stores when, in fact, less than 70% of its customers do not shop at any other sporting goods stores.
Question
Determine the Type II error if the null hypothesis, H0, is: researchers claim that 65% of college students will graduate with debt.
Select the correct answer below:
The researchers think that greater than or less than 65% of college students will graduate with debt when, in fact, 65% will graduate with debt.
The researchers think that 65% of college students will graduate with debt when, in fact, more or less than 65% of college students will graduate with debt.
The researchers think that 65% of college students will graduate with debt when, in fact, 65% of college students really will graduate with debt.
The researchers think that greater than or less than 65% of college students will graduate with debt when, in fact, greater than or less than 65% of college students will graduate with debt.
Question
Which graph below corresponds to the following hypothesis test?
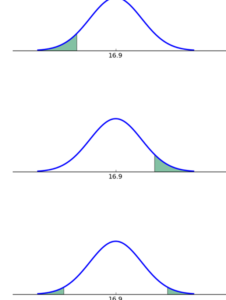
H0:μ≤16.9, Ha:μ>16.9
Second graph
Question
Which of the hypothesis tests listed below is a left-tailed test? Select all correct answers.
Select all that apply:
H0:μ≥18, Ha:μ<18
H0:μ≤19.3, Ha:μ>19.3
H0:μ=8, Ha:μ≠8
H0:μ≥11.3, Ha:μ<11.3
H0:μ≥3.7, Ha:μ<3.7
Question
Suppose a pitcher claims that her pitch speed is not equal to 45 miles per hour, on average. Several of her teammates do not believe her, so the pitcher decides to do a hypothesis test, at a 1% significance level, to persuade them. She throws 21 pitches. The mean speed of the sample pitches is 46 miles per hour. The pitcher knows from experience that the standard deviation for her pitch speed is 6 miles per hour.
- H0: μ=45; Ha: μ≠45
- α=0.01(significance level)
What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?
Solution:
Question
Jamie, a bowler, claims that her bowling score is less than 168 points, on average. Several of her teammates do not believe her, so she decides to do a hypothesis test, at a 1% significance level, to persuade them. She bowls 17 games. The mean score of the sample games is 155 points. Jamie knows from experience that the standard deviation for her bowling score is 19 points.
- H0: μ≥168; Ha: μ<168
- α=0.01(significance level)
What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?
-2.82
Question
Lexie, a bowler, claims that her bowling score is more than 140 points, on average. Several of her teammates do not believe her, so she decides to do a hypothesis test, at a 5% significance level, to persuade them. She bowls 18 games. The mean score of the sample games is 155 points. Lexie knows from experience that the standard deviation for her bowling score is 17 points.
- H0: μ≤140; Ha: μ>140
- α=0.05(significance level)
What is the test statistic (z-score) of this one-mean hypothesis test, rounded to two decimal places?
-3.74
Please click the icon below to purchase full answer at only $10
